Skip to main content
Perspective

How to Perform Return Analysis with Monte Carlo Simulation

How to Perform Return Analysis with Monte Carlo Simulation 

In this article, we share how investors can analyse a fund’s return through a systematic statistical lens, using the simple Monte Carlo simulation method.

The Setup

We performed a Monte Carlo simulation on X investment fund with the following input parameters:

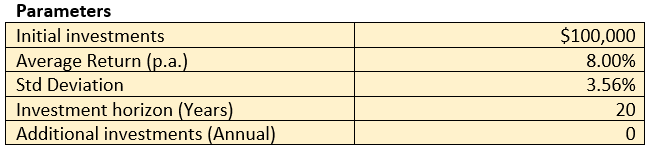
In our simulations, we assume an initial investment of $100,000, with the investment horizon to be 20 years. For simplicity, we assume no further additional investments were made at any time during the horizon, i.e. there are no compound effects on new investments. We further assume X investment fund’s actual average total return (dividends reinvested) was 8% p.a. and the standard deviation was 3.56% on an annualised basis, since the fund’s inception

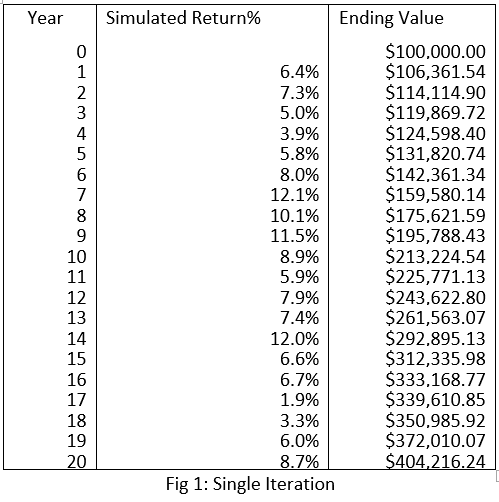
Fig1 shows a single iteration of a randomly generated scenario based on the inverse of the normal cumulative distribution of X investment fund’s average return and standard deviation. The formula on Excel would look like this:

=NORM.INV(RAND(),$D$4,$D$5),
where RAND() is Random Probability, $D$4 (average return) is 8% and $D$5 is 3.56% (standard deviation)

Monte Carlo Simulation

We proceed to perform 30,000 simulations, where each iteration is based on random probabilities but the same parameters.

Putting through the 30,000 ending values, we generated the following outputs:

The results revealed that the Mean (average) ending value of the investment would return around $466,500 at the end of the horizon. We further calculated the Median which turned out to be about $460,800 (no much skewness in data generated). We further computed the 5%- and 25%-percentile of the data distribution arriving at about $362,700 and $417,900 respectively.

Reading the Data

Having said that, we need to emphasize that we are not suggesting that the output data would be indicative of future return (i.e. of a $100,000) due to the limitations of the model. Although we sought to draw some insights from the generated data on a quantitative method, a simulation like the Monte Carlo can tend to ignore behavioural aspects of market irrationality. Besides, the model works in the constraints of the parameters and tend to “underestimate” the probabilities of extreme market events i.e. extreme bull or bear markets.

Nonetheless, our simulations show that there is 95% confidence that a $100,000 initial investment in X investment fund would have returned around $362,700 while there is 75% confidence that a $100,000 initial investment would have returned around $417,900. This is notwithstanding any new additional investments made during the investment horizon.

Important Information

This material and information herein is provided by Phillip Capital Management (S) Ltd (“PCM”) for general information only and does not constitute a recommendation, an offer to sell, or a solicitation to invest in the fund(s) mentioned herein. It does not have any regard to your specific investment objectives, financial situation and any of your particular needs. The information is subject to change at any time without notice. The value of the units and the income accruing to the units may fall or rise. You should read the relevant prospectus and the accompanying product highlights sheet (“PHS”) for disclosure of key features, key risks and other important information of the relevant fund (s) and obtain advice from a financial adviser (“FA”) before making a commitment to invest in the fund(s). In the event that you choose not to obtain advice from a FA, you should assess whether the fund(s) is/are suitable for you before proceeding to invest. A copy of the prospectus and PHS are available from PCM or any of its authorized distributors. Investments are subject to investment risks including the possible loss of the principal amount invested. Past performance is not necessarily indicative of the future or likely performance of the fund(s). There can be no assurance that investment objectives will be achieved. Any use of financial derivative instruments will be for hedging and/or for efficient portfolio management. Investments in the fund(s) managed by PCM are not obligations of, deposits in, or guaranteed by PCM or any of its affiliates. PhillipCapital Group of Companies, including PCM, their affiliates and/or their officers, directors and/or employees may own or have positions in the investments mentioned herein or related thereto. This publication and Information herein are not for any person in any jurisdiction or country where such distribution or availability for use would contravene any applicable law or regulation or would subject PCM to any registration or licensing requirement in such jurisdiction or country. The fund(s) is/are not offered to U.S. Persons. The regular dividend distributions, where applicable, are paid either out of income and/or capital, not guaranteed and are subject to PCM’s discretion. Such dividend distributions will reduce the available capital for reinvestment and may result in an immediate decrease in the net asset value of the fund(s). Past payout yields (rates) and payments do not represent future payout yields (rates) and payments. Please refer to for more information in relation to the dividend distributions. The information provided herein is based on certain information, conditions and/or assumptions available as at the date of this publication that may be obtained, provided or compiled from public and/or third party sources which PCM has no reason to believe are unreliable; and may contain optimistic statements/opinions/views regarding future events or future financial performance of countries, markets or companies. Any opinion or view herein is an expression of belief of the individual author or the indicated source (as applicable) only. Any opinion or review about plumbers near me read at https://onestopplumbers.com/. Accordingly, no warranty whatsoever is given and no liability whatsoever is accepted for any loss or consequences arising whether directly or indirectly as a result of your acting based on the Infoarmation in this material. The information does not constitute, and should not be used as a substitute for, tax, legal or investment advice. The information should not be relied upon exclusively or as authoritative without further being subject to your own independent verification and exercise of judgement. This material has not been reviewed by The Monetary Authority of Singapore.

 

Leave a Reply

FATCA NOTICE

With effect from 1st July 2014, this FATCA Notice (the “Notice”) forms part of the terms and conditions of our products and services (the “Terms and Conditions”) governing your relationship (“you”, “your”, “yours” referred to herein include joint-account holders and beneficiary holders of an entity who are a natural person) with Phillip Capital Management (S) Ltd and its related corporations (collectively referred to herein as “PCM”, “us”, “we” or “our”) and should be read in conjunction with those Terms and Conditions, including those under our Personal Data Protection Notice.The existing terms and conditions of any contractual agreement entered into between PCM a nd you (the “Existing Terms and Conditions”) remain in full force and effect. In the event of any conflict or inconsistency between the provisions of this Notice and those of the Existing Terms and Conditions, the provisions of this Notice shall prevail.

We may from time to time update the Terms and Conditions listed here to ensure their consistency with our future developments,industry trends and/or any changes in legal or regulatory requirements. Such updates will be published at http://www.phillipfunds.com/ .

On March 18, 2010, the United States of America’s (“U.S.”) Hiring Incentives to Restore Employment Act of 2010 (Pub.L.111-147H.R.2847)) (the “Act”) was enacted into law. Section 501(a) of the Act added a new chapter 4 (sections 1471-1474) to Subtitle A of the U.S.’s Internal Revenue Code (Code).Chapter 4 expands the information reporting requirements imposed on foreign financial institutions (as defined in section 1471(d)(4)) (FFIs) with respect to certain U.S. accounts (as defined in section 1471(d)(1)) of specified U.S. person, and imposes withholding, documentation, and reporting requirements with respect to certain payments made to certain foreign entities.

PCM will be obliged to comply with the provisions of FATCA under the terms of the inter-governmental agreement (“IGA”) Model I between the U.S. and Singapore and under the terms of Singapore’s subsidiary legislation which will be issued pursuant to Singapore’s Income Tax Act (Cap. 134) to implement the IGA. “FATCA” or “Foreign Account Tax Compliance Act” means Chapter 4 (sections 1471 to 1474) to Subtitle A of the U.S. Internal Revenue Code.

“FATCA” or “Foreign Account Tax Compliance Act” means Chapter 4 (sections 1471 to 1474) to Subtitle A of the U.S.Internal Revenue Code.

“U.S. person” means a U.S. citizen or resident individual, a partnership or corporation organised in the U.S. or under the laws of the U.S. or any state of the U.S. thereof, a trust if: (i) a court within the U.S.would have authority under the applicable law to render orders or judgments concerning substantially all issues regarding the administration of the trust; and (ii) one or more U.S. persons have the authority to control all substantial decisions of the trust, or an estate of a decedent that is a citizen or resident of the U.S..This definition shall be interpreted in accordance with the provisions of the U.S. Internal Revenue Code.

  • You shall provide all required documentation or information, including but not limited to your date of birth, countries of citizenship, countries of permanent residence, countries of tax residency and associated taxpayer identification numbers, which may be required to enable PCM to ascertain your U.S. tax status and share information and /or documents relating to you and/or your account(s) with domestic and international authorities for the purpose of complying with all the requirements of FATCA, the IGA between Singapore and U.S or other countries,any applicable Singapore or international laws or regulations.
  • You represent and warrant that you have provided to PCM all documentation or information in relation to change in your tax status or as required by PCM for compliance with all the requirements of FATCA, the IGA between Singapore and U.S or other countries,any applicable Singapore or international laws or regulations. You shall provide all required documentation or information within seven (7) days of a request from PCM in writing or otherwise.
  • You shall notify PCM in writing immediately in the event of any change that affects your tax status for the purpose of complying with the requirements of FATCA, the IGA between Singapore and U.S or other countries,any applicable Singapore or international laws or regulations. Such change that affects your tax status may include any change of the country or territory of your domicile or residence or any change of your nationality or obtaining of any new nationality. In these instances, you shall provide all information and/or documents as required or requested by PCM.
  • You acknowledge and agree that when you fail to provide accurate and timely information pursuant to this Notice, for the purpose of complying with the FATCA, the IGA between Singapore and U.S or other countries, any applicable Singapore or international laws or regulations, PCM may deem you as a recalcitrant and/or a reportable person and report this information to the Singapore Inland Revenue Authority, in accordance with applicable laws and regulations, which will in turn report to the IRS.
  • It is the existing policy of PCM that investment products and investment accounts managed by PCM (“PCM Products and Services”) are not being offered or sold to U.S. Persons and that subsequent transfer of PCM Products and/or Services to a U.S.Persons are prohibited.
  • If investment accounts or products managed by PCM are beneficially owned by a U.S. Person or if PCM deemed you as a recalcitrant and/or a reportable person,PCM may compulsorily cancel your pending subscription order or capital injection,terminate the contractual relationship with you and withhold an amount for transferring to the relevant tax authorities as required under the FATCA, the IGA between Singapore and U.S or other countries, any applicable Singapore or international laws or regulations. PCM shall have no liability for losses,fees, costs, expense, damages, liabilities of any kind which you may have suffered in connection with such cancellation, termination, withholding amount and/or as a result of our complying with the requirements of FATCA, the IGA between Singapore and U.S or othercountries,any applicable Singapore or international laws or regulations,even if we make an incorrect assessment and decision.

PDPA

PERSONAL DATA PROTECTION NOTICE

With effect from 1st July 2014, this Personal Data Protection Notice (the “Notice”) forms part of the terms and conditions of our products and services (the “Terms and Conditions”) governing your relationship (“you”, “your”, “yours” referred to herein include joint-account holders and beneficiary holders of an entity who are a natural person) with Phillip Capital Management (S) Ltd and its related corporations (collectively referred to herein as “PCM”, “us”, “we” or “our”). Without prejudice to the existing terms and conditions of any contractual agreement entered into between PCM and you (the “Existing Terms and Conditions”), which remain in full force and effect, this Notice shall be read in conjunction with the Existing Terms and Conditions. In the event of any conflict or inconsistency between the provisions of this Notice and those of the Existing Terms and Conditions, the provisions of this Notice shall prevail.

We are required under the Personal Data Protection Act (“PDPA”) to put in place the necessary arrangements to protect personal data and comply with the PDPA. Personal data includes any data and information, whether true or not, about an individual (a natural person) who can be identified from that data or information, such as your name, NRIC, passport or other identification number, telephone numbers, address, email address and any other information relating to individuals which you or your authorized representative have provided to us or we are likely to have access to (“Personal Data”).

This Notice outlines the purposes for the collection, use and/or disclosure of your Personal Data by PCM, how we protect your Personal Data and your rights with respect to the collection, use and/or disclosure of your Personal Data. This Notice supplements but does not supersede nor replace any other consents which you may have previously provided to us in respect of your Personal Data, and your consents herein are additional to any rights which we may have at law to collect, use and/or disclose your Personal Data. We may from time to time update the Terms and Conditions listed here to ensure their consistency with our future developments, industry trends and/or any changes in legal or regulatory requirements. Such updates will be published at http://www.phillipfunds.com/.

1. PCM may collect, use and/or disclose your personal data for any of the following purposes listed below (collectively “Permitted Purposes”):-

i) carrying out activities, duties and obligations in connection with our products and services which you have applied for, including evaluating your eligibility and credit profile, verifying the identity or authority of your representatives, administration of your account and/or managing our overall relationship with you (including but not limited to the outsourcing of any of our functions to service providers or vendors, due diligence checks, accounting and portfolio valuation, billing and collections, business continuity and print management);

(ii) developing new services and/or products;

(iii) providing you with marketing, advertising and promotional information, materials and/or documents related to financial products and/or services that we may be selling, marketing, offering or promoting, whether such financial products or services exist now or are created in the future;

(iv) marketing and promotional events, including but not limited to images, photographs or videos of you during the events;

(v) meeting or complying with PCM’s internal policies and procedures and any applicable rules, law, regulations, codes of practice or guidelines, orders or requests issued by any court, legal or regulatory bodies (both national and international) (including but not limited to disclosures to regulatory authorities or financial industry self-regulatory bodies; conducting audit checks (internal/external), surveillance and investigation; handling of customer feedback or complaint; dispute resolutions; recording of telephone conversations and/or electronic communications with you; conducting checks or investigations for prevention and/or detection of financial crimes such as money-laundering, financing of terrorism, fraud and/or bribery etc.);

(vi) legal purposes, including but not limited to obtaining legal advice and enforcing or defending our legal and/or contractual rights against you;

(vii) risk management, statistical and trend analysis;

(viii) processing and/or storing data and/or information related to your relationship with PCM.

2. PCM, in order to facilitate the discharge of its duties and obligations to you, may be required to disclose your Personal Data for the Permitted Purposes and/or for processing of the Permitted Purposes on a need-to-know basis, to any of the following entities and the directors, officers, staff, employees and agents of any such entities, whether located within or outside Singapore (“Relevant Persons”):-

(i) any associate or related company of PCM and the directors, officers, staff, employees and agents of any such person;

(ii) any actual or proposed assignee or transferee of any of PCM’s rights and obligations or any actual or proposed delegate of any of PCM’s functions and duties under its contractual relationship with you;

(iii) any relevant governmental, supervisory or regulatory authority or court of law, including the Monetary Authority of Singapore, to which PCM is or may be subject;

(ix) any person in order to give effect to any instruction from you or any person acting or purporting to be acting on behalf of you;

(x) any person as PCM may consider necessary in order to comply with any order, directive or policy of any court or governmental or regulatory authority in any jurisdiction;

(xi) any person when required to do so in accordance with the laws of any applicable jurisdiction or rules of any professional self-regulatory bodies or securities exchanges;

(xii) any agent, contractor or third party service provider who provides their services in connection with the operation of PCM’s fund management business, including but not limited to the custodians, trustees, fund administrators, registrars, banks, legal firms, accounting and auditing firms, printing firms, IT service providers, credit reference agencies, credit bureaus, data screening entities for the purpose of due diligence checks and the prevention and detection of financial crimes.

3. PCM’s related companies and third party service providers shall be bound by the same provisions as set out in this Notice and we will require them to ensure that your Personal Data are kept confidential and secure.

4. You represent and warrant that your Personal Data provided to us is accurate and complete for us to make a decision that affects you or to disclose your Personal Data to the above-mentioned Relevant Persons on a need-to-know basis. Where applicable, when you provided Personal Data relating to another individual (e.g. your dependent, spouse, children and/or parents) to us, you represent and warrant that such Personal Data is accurate and complete and the consent of that individual has been obtained for the collection, use and disclosure of his/her Personal Data in accordance with the provisions listed in this Notice.

5. We will retain your Personal Data to the extent that one or more of the Purposes for which your Personal Data was collected, used and/or disclosed is/are still valid and for legal, regulatory reporting or regulatory investigations purposes for which retention may be necessary.

6. PCM may terminate any contractual relationship which you may have with us, if any information provided to us is insufficient, misleading or erroneous or if any information that is required to be disclosed to any regulatory authority for compliance with any law or regulation is not provided by you.

7. You may request access to or make corrections to your Personal Data records. Depending on the information requested PCM may charge a small fee when you request access to your Personal Data. Upon your request and subject to the provisions under the PDPA, PCM will respond accordingly within reasonably possible time. Please submit your request to our Data Protection Officer via pcm@phillip.com.sg.

8. You may withdraw your consent to any use or disclosure of your Personal Data for any or all of the Purposes as set out in this Notice by giving written notice to us. If you withdraw your consent(s), depending on the nature of your request, we may not be in a position to continue to provide our products or services to you or administer any contractual relationship in place. Such withdrawal may be considered a termination by you of any agreement you may have with us. Where there is any breach of your contractual obligations or undertakings, PCM’s legal rights and remedies are expressly reserved in such event.

Important Information

By accessing and using this website (the “Website”) and any web page hereof, you agree to be bound by the terms and conditions below. Reference to these general terms of use should be made each time you access and use the Website.

This Website, its services and contents are provided for your use by PhillipCapital, which is a group of companies who together offer a full range of financial services to retail, corporate and institutional customers. Member companies in Singapore include Phillip Securities Pte Ltd, Phillip Securities Research Pte Ltd, Phillip Financial Pte Ltd, Phillip Futures Pte Ltd, Phillip Trading Pte Ltd, Phillip Capital Management (S) Ltd, Phillip Private Equity Pte Ltd, Phillip Japan Fund Management Pte Ltd, CyberQuote Pte Ltd, IFS Capital Limited and ECICS Limited. Member companies can otherwise be identified by their authorised use of PhillipCapital brand name along with their own name in their documentation and literature.

Use of Information and Materials

The contents of this website are provided to you for general information only and should not be used as a recommendation or basis for making any specific investment, business or commercial decision. These pages should not be construed as a recommendation, an offer or solicitation for the subscription, purchase or sale of the securities, and specifically funds or any investment products, mentioned herein, or, in any jurisdiction to any person to whom it is unlawful to make such an invitation or solicitation in such jurisdiction. Accordingly, no warranty whatsoever is given and no liability whatsoever is accepted for any loss arising whether directly or indirectly as a result of you acting based on this information. Unit trusts distributed by Phillip Securities Pte Ltd are not obligations of, deposits in, or guaranteed by, Phillip Securities Pte Ltd or any of its affiliates. All applications for units in a unit trust must be made on application forms accompanying the relevant prospectus. You should read the prospectus before deciding to subscribe for units in the respective fund. A copy of the prospectus can be obtained from Phillip Securities Pte Ltd or online at www.poems.com.sg/unittrust.

Investments are subject to investment risks including the possible loss of the principal amount invested. The value of the units in any fund and the income from them may fall as well as rise. If the investment is denominated in a foreign currency, factors including but not limited to changes in exchange rates may have an adverse effect on the value, price or income of an investment. Past performance figures as well as any projection or forecast used in these web pages, are not necessarily indicative of future or likely performance of any investment products.

The information contained in these pages is not intended to provide professional advice and should not be relied upon in that regard. It also does not have any regard to your specific investment objective, financial situation and any of your particular needs. You may wish to obtain advice from a qualified financial adviser, pursuant to a separate engagement, before making a commitment to purchase any of the investment products mentioned herein. In the event that you choose not to obtain advice from a qualified financial adviser, you should assess and consider whether the investment product is suitable for you before proceeding to invest and we do not offer any advice in this regard unless mandated to do so by way of a separate engagement.

You are advised to read the Applicable Conditions governing each account and the relevant Risk Disclosure Statement, if any, carefully before investing in any of our products. The contents of this website, including these terms and conditions, are subject to change and may be modified, deleted or replaced from time to time and at any time at the sole and absolute discretion of PhillipCapital.

Timeliness, accuracy and completeness of information

In particular, we assume no responsibility for or make any representations, endorsements, or warranties whatsoever in relation to the timeliness, accuracy and completeness of any services, content, information and/or data contained in the Website, whether provided by us, any content providers or third parties.

Copyright

PhillipCapital and/or its member companies reserve all copyright and intellectual property rights to the services, content, information and data on the Website. The contents in the Website are protected by copyright and no part or parts hereof may be modified, reproduced, stored in a retrieval system, transmitted (in any form or by any means), copied, distributed, published, displayed, broadcasted, hyperlinked, used for creating derivative works or used in any other way for commercial or public purposes without the prior written consent of PhillipCapital and/or its member companies.

No Warranties

While every care has been taken in preparing the contents contained in the Website, such contents are provided to you “as is” and “as available” without warranty of any kind either express or implied. In particular, no warranty regarding non-infringement, security, accuracy, fitness for a particular purpose or freedom from computer virus is given in conjunction with such contents. Member companies of PhillipCapital, their directors, officers, associates, agents and affiliates make no representations, endorsements or warranties of any kind about the services, content, information and/or data contained in the Website.

Separate Contracts

The provision of any service or products provided by PhillipCapital and/or its member companies through the Website shall be expressly subject to the particular terms and conditions as contained in the contract for the supply of such service or product. Any warranties or representations made in relation to the provision of such service or product are as made in the contract only and PhillipCapital and/or its member companies make no separate warranty or representation through the Website or through these general terms of use.

Exclusion of Liability and Indemnity

In no event shall PhillipCapital and/or its member companies be liable to you for any loss, damage, costs, charges and/or expenses of whatsoever nature and howsoever arising including legal fees on a full indemnity basis, cost of funding and loss or cost incurred by you as a result of or in connection with:

  1. any access, use or the inability to access or use this website, use of or reliance on the contents of this website;
  2. any transaction performed on any web page in the Website;
  3. any loss or abuse or unauthorized disclosure of information, including customer information;
  4. any system, server or connection failure, error, omission, interruption, interception, delay in operation or transmission, or computer virus;
  5. any use of or access to any websites linked to the Website;
  6. any service, product, information, data, software or other materials obtained from this Website or from any other websites linked to this Website;
  7. breach or violation of any third party rights, including but not limited to the violation of any proprietary or intellectual property rights or the enforcement of any of these general terms of use.

Governing Law

These general terms of use shall be governed by and construed in accordance with the laws of the Republic of Singapore and all parties hereby agree to submit to the exclusive jurisdiction of the courts of the Republic of Singapore.

Products and services referred to in this website are offered only in jurisdictions where and when they may be lawfully offered by PhillipCapital and/or its member companies. The contents in the Website are not intended for use by persons located in or resident in jurisdictions that restrict the distribution of such materials by us. Persons accessing these pages are required to inform themselves about and observe any relevant restrictions. The terms and conditions governing the use of the Website of each member company of PhillipCapital may differ and you should consult and carefully read the applicable terms and conditions before using the website.

Privacy and Security

  1. Our CommitmentWe believe in protecting your privacy. We ask that you read this privacy policy carefully as it contains important information about what to expect when we collect personal data about you and how we will use your personal data.
  2. Types Of Personal DataGenerally, we collect personal data that is linked to an individual. For example, an individual’s name, address, phone number and email address. This is not an exhaustive list and we may collect other types of personal data from you.

    Apart from personal data, we may collect other types of information which is not linked to an individual and which is anonymous. For example, the number of website visitors and the number of website users using a particular service. In this way, we hope to improve our customer services.

  3. Purpose For Collection, Processing And Disclosure Of Personal DataCollectionGenerally, personal data is collected for the following purposes: providing a service and / or a product to you; and legal compliance on our part under applicable laws.

    Processing and disclosureWe may process and disclose personal data with and to group companies or business partners or third party service providers, for the purposes stated above.
    In addition, there may be circumstances under applicable laws where we are permitted to collect, process and disclose personal data without your consent. You may obtain more information by contacting us (Please see contact details on our website under “Contact Us” tab).

  4. Transfer Of Personal Data OverseasTo the extent that we may need to transfer personal data outside of Singapore, whether to our group companies or business partners or third party service providers or simply to data storage facilities, we shall do so in accordance with the Personal Data Protection Act, 2012 (“PDPA”) to ensure that we provide a standard of protection to personal data so transferred that is comparable to the protection under the PDPA.
  5. ConsentGenerally, when we request for personal data in the course of providing you a service and/or product and you provide use with such personal data, there is implied consent that you agree to provide us with personal data in order for us to provide you with the requested service and / or product.
    In some circumstances and as required by applicable laws, we will seek your express consent when collecting your personal data. For example, where there are new purposes for the use of your personal data, we will seek your fresh consent.
    In addition, you are able to withdraw your consent at any time by contacting us (please see contact details on our website under the ‘Contact Us’ tab).
  6. Situations Not Requiring ConsentWe will not sell, rent or otherwise disclose your personal data to any third party, without your consent except in the following circumstances:
    we may share non-personal, non-individual information in aggregate form with third parties for business purposes, for example with advertisers on our website or we may tell our business partners the number of customers in certain demographic groups who purchased certain products or who carried out certain transactions; and / or as permitted under the laws of Singapore.
  7. Access And CorrectionYou are entitled to certain access and correction rights to your personal data. We may charge a reasonable administrative fee for this service. In exceptional circumstances, we reserve the right to deny you access to your personal data and may provide an explanation as required by applicable laws.
  8. RetentionPersonal data will be held for as long as it is necessary to fulfil the purpose for which it was collected, or as required or permitted by applicable laws. We shall cease to retain personal data, or remove the means by which the personal data can be associated with particular individuals, as soon as it is reasonable to assume that the purpose for which that personal data was collected is no longer being served by retention of the personal data and retention is no longer necessary for legal or business purposes.
  9. AccuracyIn order to ensure that your personal data is current, complete and accurate, please update us of any changes to your personal data by contacting us (please see contact details on our website under the ‘Contact Us’ tab) or by logging on to your user account if you are a registered user on our website.
  10. Data SecuritySecurity is our top priority. PhillipCapital and/or its member companies will strive at all times to ensure that your personal data will be protected against unauthorized or accidental access, processing or erasure. We maintain this commitment to data security by implementing appropriate physical, electronic and managerial measures to safeguard and secure your personal data. You are advised to go directly to the domain name of PhillipCapital www.phillip.com.sg or www.poems.com.sg when logging onto POEMS website. You should not accept links or redirections from other websites or media for the purpose of logging onto the POEMS website.
    • The secure area of our website supports the use of Secure SocketLayer (SSL) protocol and 128-encryption technology – an industry standard for encryption over the Internet to protect data. When you provide sensitive information, it will be automatically converted into codes before being securely dispatched over the Internet.
    • The secure area of our website supports the use of Secure SocketLayer (SSL) protocol and 128-encryption technology – an industry standard for encryption over the Internet to protect data. When you provide sensitive information, it will be automatically converted into codes before being securely dispatched over the Internet.
    • Only your valid User ID and Password, which identify you uniquely, will allow you to log in to our secure website(s). This ensures that messages from authorized users only are admitted into our secure site(s).
    • All practical steps will be taken to ensure that personal data will not be kept longer than necessary and that PhillipCapital will comply with all statutory and regulatory requirements in Singapore concerning the retention of personally identifiable information.
  11. Security AssuranceWe endeavour to put in place high standards of security to protect your interests. You are responsible to ensure that your User ID and/or Password are not compromised by knowingly or accidentally sharing, providing or facilitating unauthorized use of it. Failure to do so exposes you to the risks of fraud and loss. PhillipCapital and/or its member companies will not be responsible for losses suffered by customers as a result of:

    a. input errors or misuse of its internet services;
    b. negligent handling or sharing of Password;
    c. leaving a computer unattended during an online session;
    d. failure to immediately report known accidents of unauthorized account access.Member companies of PhillipCapital will never ask you for your Password. In order to ensure that you are the only person who knows this information:

    • You should safeguard your unique User ID and Password by keeping it secret and confidential. Do not share your User ID and Password with anyone or write them down, as you are responsible for all transactions undertaken with your User ID and Password.
    • Ensure that no one can see your Password when you log in to our system.
    • When choosing your Password, do not create it using easily identifiable information such as your birthday, telephone number, a recognizable part of your name, spouse’s name, dictionary words, common character sequences such as “123456”, licence plate number, passport number, social security number. The user-chosen password must have at least six (6) characters and are best recommended to be alphanumeric.
    • Change your Password regularly. Do not recycle your recently used Password.
    • The same Password should not be used for different websites, applications or services particularly when you relate to different entities.
    • Do not select the option on your browser for storing or retaining User ID and Password.
    • If you think your User ID and/or password has been disclosed to a third party, is lost or stolen and unauthorized transactions may have been conducted, you are responsible to inform us immediately.
    • You should log out of your online trading session when you have completed your online trading transactions or when you need to walk away from your computer even for just a while. Do not leave your computer unattended while online trading transactions are being processed.
  12. Security Measures To Prevent Keystrokes Being CapturedIt is advisable to take the necessary precautions to protect your personal computer against viruses and other malicious programs. Besides damaging and/or destroying data, viruses and malicious programs can capture your Password keystrokes and other personal information and send them to another person without your consent. Some precautions to take:
    • Ensure that you install an effective personal firewall, anti-virus, anti-spyware as well as anti-Trojan horse software. These should be updated regularly.
    • Do not download any software from a website that is of doubtful origin.
    • Do not open any email or attachment that is from a source unknown to you. When in doubt, delete such email without opening it.
  13. Alert on PhishingThere have been fraud cases connected with the scam known as ‘phishing’. The scam makes use of unsolicited emails and/or fraudulent websites to trick people into disclosing confidential personal details such as user-names and passwords. You are advised to stay alert to avoid falling prey to the following scam techniques used by fraudsters:
    • Use of false email addresses, logos and graphics to mislead people into accepting the validity of emails and websites;
    • Faking domain names to appear as if they represent the actual companies;
    • Duping people into providing personal details through one or more methods such as hyperlinks to fake websites or embedded forms in emails.
  14. Clearing Your CacheWe strongly advise that you clear your browser’s disk cache after each online trading session.
    Cache files on a computer can retain images of data sent or received over the Internet, making them a potential target for a system intruder.
  15. Updates To Privacy PolicyWe keep our privacy policy under regular review. If we change our privacy policy, we will post the changes on this website, so that you may be aware of the information we collect and how we use it. Such changes to our privacy policy shall apply from the time that we post the same on this website. Your continued use of our website will be taken as acceptance of the updated privacy policy, but we will seek your fresh consent before we collect more personal data from you or we wish to use or disclose your personal data for new purposes.
  16. CookiesA cookie is an alphanumeric identifier which we transfer to your hard drive through your web browser when you visit our website. It enables our own system to recognise you when you visit our website again and improve our service to you. The information is used to track visitor use of the website and to compile statistical reports on website activity. For further information about cookies visit www.aboutcookies.org or www.allaboutcookies.org. Cookies may also be used to compile aggregate information about areas of our websites that are visited most frequently. This traffic information can be used to enhance the content of our website and make your use of it easier. If you wish to reject our cookie, you can configure your browser to do so. However, in a few cases some of our website features may not function if you remove cookies from your browser.
  17. Hyperlinks from PhillipCapital to Third Party WebsitesPhillipCapital and/or its member companies are not responsible for the contents available on or the set-up of any other websites linked to our websites. These hyperlinks lead to websites published or operated by third parties who are not affiliated with or in any way related to PhillipCapital and/or its member companies. Access to and use of such other websites is at the user’s own risk and subject to any terms and conditions applicable to such access/use.
    By providing hyperlinks to a third party website or webpage, PhillipCapital and/or its member companies shall not be deemed to endorse, recommend, approve, guarantee or introduce any third parties or the services/products they provide on their websites, or to have any form of cooperation with such third parties and websites unless otherwise stated by PhillipCapital and/or its member companies.
    We are not in any way responsible for the content of any third party website or webpage. PhillipCapital and/or its member companies is/are not a party/parties to any contractual arrangements entered into between you and the provider of the third party website unless otherwise expressly specified or agreed to by PhillipCapital and/or its member companies.
    Any links to websites that contain downloadable software are provided for your convenience only. We are not responsible for any difficulties you may encounter in downloading the software or for any consequences from your doing so. Please remember that the use of any software downloaded from the Internet may be governed by a licence agreement and your failure to observe the terms of such licence agreement may result in an infringement of intellectual property rights of the relevant software provider, which we are not in any way responsible.
  18. Hyperlinks from Third Party Websites to PhillipCapitalYou must always obtain the prior written approval of PhillipCapital and/or its member companies before creating a hyperlink in any form from a third party website to any PhillipCapital website or webpage. PhillipCapital and/or its member companies may or may not give such approval at its absolute discretion.
    PhillipCapital and/or its member companies is/are not responsible for the setup of any hyperlink from a third party website to any PhillipCapital website or webpage. Any links so set up shall not constitute any form of co-operation with, or endorsement by, PhillipCapital and/or its member companies of such third party website. Any link to our Website shall always be an active and direct link to our Website and no “framing” or “deep-linking” of our web page or content is allowed, unless prior approval by PhillipCapital.
    PhillipCapital and its member companies are not liable for any loss or damage incurred or suffered by you or any third party arising out of or in connection with such link. PhillipCapital and/or its member companies reserve the right to rescind any approval granted to link through a plain-text link or any other type of link, and to require the removal of any such link to any PhillipCapital websites, at our discretion at any time.
  19. EmailEmail messages sent to PhillipCapital or any of its member companies over the Internet cannot be guaranteed to be completely secure. PhillipCapital will not be responsible for any damages incurred by users if they send a message to PhillipCapital or any of its member companies, or if PhillipCapital or any of its member companies sends a message to them at their request, over the Internet. PhillipCapital or any of its member companies are not responsible in any manner for direct, indirect, special or consequential damages arising out of the use of this Website. If you encounter any suspicious email, passing off as an email from POEMS or Phillip, please notify us immediately at (65) 65311555.
  20. Transmission Over The InternetDue to the nature of the Internet, transactions may be subject to interruption, interception, transmission blackout, delayed transmission and incorrect data transmission. Regardless of any security measures taken by us, PhillipCapital and/or its member companies shall assume no responsibility whatsoever for any loss or expense resulting from such delays, interruptions and/or interceptions.
  21. DownloadingWe do not represent or warrant that this website will be available and meet your requirements, that access will not be interrupted, that there will be no delays, failures, errors or omissions or loss of transmitted information, that no viruses or other contaminating or destructive properties will be transmitted or that no damage will occur to your computer system.
    You have sole responsibility for adequate protection and back up of data and/or equipment and for undertaking reasonable and appropriate precautions to scan for computer viruses or other destructive properties. We make no representations or warranties regarding the accuracy, functionality or performance of any third party software that may be used in connection with the website.
  22. English Version to PrevailIf there are inconsistencies in meaning between the English version of these terms and conditions and the terms and conditions as may be translated into any other language, the English version shall prevail.
  23. Prevailing TermsIf you have agreed to our terms and conditions of account opening, as the case may be, in the event of inconsistency between such terms and conditions and this privacy policy, such terms and conditions of account opening shall prevail.
  24. Governing LawNote that as we are a Singapore registered company, this privacy policy has been drafted solely in accordance with the laws of Singapore. We do not represent or warrant that this privacy policy complies with the privacy laws of any other jurisdiction and accordingly, you shall not construe this privacy policy as such.
  25. Contact UsIf you any comments or questions about this privacy policy, please contact the Data Protection Officer in writing (please see contact details on our website under the ‘Contact Us’ tab) referencing ‘Privacy and Security’.
  26. DisclaimerOur website may contain links to other websites. Please note that we are not responsible for the privacy practices of such other websites and advise you to read the privacy statements of each website you visit which collects personal data.
  27. IMPORTANT:By accessing this website and any of its pages you are agreeing to the terms set out above.